Crystal growth Monte Carlo – evan-freeland.com

The programs associated with this project can be found on my Github, github.com/ELFREELAND/vapor_dep_monte_carlo

What is crystal growth?

Modern electronics are enabled by the ability to grow large crystals with minimal defects and impurities. This is typically done by creating a solid crystal from a fluid precursor. For example, silicon wafers for microprocessors are created by carefully solidifying a boule out of a vat of molten silicon. Monopotassium phosphate¹ crystals are grown by dissolving the compound in water and crystallizing them from solution. And the semiconductors used for LEDs are deposited from a vapor.

What is Monte Carlo?

Monte Carlo is a type of simulation that works by generating random numbers (it’s named after the famous casino in Monaco). For example, by inscribing a circle with diameter 2 inside a square of side length 2, and generating many random points within the square, and counting what fraction fall within the circle, you can get a numerical value of $\frac{\pi}{4}$ . As far as calculations of $\pi$ go, this is rather inefficient, but for other investigations, a Monte Carlo simulation may be the best approach available.

This project

The goal is to make a Monte Carlo simulation of crystal growth. There are two main phenomena that I want to capture: condensation and migration. Condensation means atoms are arriving at the surface from the fluid. Migration means the atoms on the surface are moving around. I will assume the crystal has a simple cubic structure, so the surface can be represented by a grid of numbers (with periodic boundary conditions), where each number represents the height of the surface at that point. This is called a solid-on-solid model. To add an atom to the surface, one of the grid points can be chosen at random and increased by one. To move an atom, two adjacent grid points can be chosen at random, and one of them can be increased by one while the other is decreased by one.

This is an idea that has been tried before (see references), usually with more rigor than what is attempted here, but there is one thing that all the papers lack: animations. I want to see the behavior of each individual atom, not just the still images and statistics that are given in the papers I’ve seen. My goal here is mostly to make pretty pictures rather than conduct a rigorous scientific investigation, so I will make some assumptions out of convenience rather than realism.

How the simulation works

I will assume atoms arrive on the surface with Poisson statistics. On each cycle of the simulation, a Poisson-distributed random number will be chosen with mean $j$ , and that many atoms will arrive on the surface.

I will assume the rate at which an atom migrates in a lattice follows the Arrhenius equation $e^{-\frac{E_m}{k_bT}}$ , where $E_m$ is the activation energy for migration, $k_b$ is Boltzmann’s constant, and $T$ is temperature. In the case of surface diffusion, $E_m$ can be interpreted as “the energy required to break the bonds of the atom with its neighbors”. I will get $E_m$ by counting how many neighbors an atom has, $n$ , and multiplying by the energy per bond, $E_b$ . Every atom will have a chance of $p_m=e^{-\frac{nE_b}{k_bT}}$ to migrate on every cycle of the simulation.

The fact that the number of bonds factors into the migration probability is important. It means it is harder for an atom to leave some positions than others. Consider the following image:

The 3 labeled atoms are labeled with the number of bonds they have with their neighbors. It is really easy for atom 1 to move, because it only needs to break 1 bond. It is hard for atom 3 to move, because it has to break 3 bonds. Sometimes it is easier to get into a position than to get out of it, or vice versa. If atom 3 moved up to be next to atom 2, it would have to break 3 bonds, but if it went back to its original position, it would only have to break 2 bonds. This is very important because it means certain configurations of atoms are more stable than others. When there are not enough atoms to form a complete layer, they tend to form clusters on the surface, since an atom in the cluster would have to break 2, 3, 4, or 5 bonds to leave the cluster, but probably only 1 bond to join the cluster. Therefore a flat cluster of atoms is more stable than a bunch of atoms scattered around the surface, and also more stable than a pile of atoms more than 1 layer thick. As more atoms arrive at the surface, the clusters grow and merge together to form a complete layer. In this way, atomic layers tend to form one at a time, resulting in a surface that stays smooth as the crystal grows. This layer-by-layer growth can only happen under certain conditions, though, as these simulations will show.

Diffraction intensity

Some crystal growth techniques have the advantage that you can use in-situ characterization to monitor the progress of the growth. One of these techniques is reflection high-energy electron diffraction (RHEED), which works by shooting a high-energy electron beam at the surface of the crystal at a glancing angle, and collecting the reflected beam on a phosphor screen to view the patterns created by the surface atomic structure of the crystal. Because of the use of an electron beam, this technique is restricted to use in ultra high vacuum.

One cool thing about RHEED is that if you grow the crystal just right, the intensity of the reflection will oscillate with every individual atomic layer that deposits on the crystal, so you can individually count the atomic layers. One textbook (Tsao, 1993, see references) suggests an equation for a simplified idea of reflected beam intensity from a surface, which i’ve simplified further here:

$I=\left(\sum_i (-1)^i\theta_i\right)^2$

where $\theta_i$ is the fraction of the surface that is covered to a depth $i$ . The idea here is that the electrons reflected from layer $i$ will destructively interfere with those reflected from layer $i+1$ , $i-1$ , $i+3$ , $i-3$ etc., and constructively interfere with those reflected from layer $i+2$ , $i-2$ , $i+4$ , $i-4$ , etc.; i.e. there is destructive interference between electrons reflected from adjacent layers and constructive interference between electrons reflected from layers separated by 2.

This serves as a measure of the smoothness of the surface – a rough surface will have a $I$ near 0, while a perfectly smooth surface will have $I=1$ . If the crystal is growing layer-by-layer, $I$ will oscillate with the formation of new layers.

Simulations

I have coded the simulations in C, and used Python’s matplotlib library to make animations of the crystal growth². Here is an example, with $j=2$ and $\frac{E_b}{k_bT}=2$ :

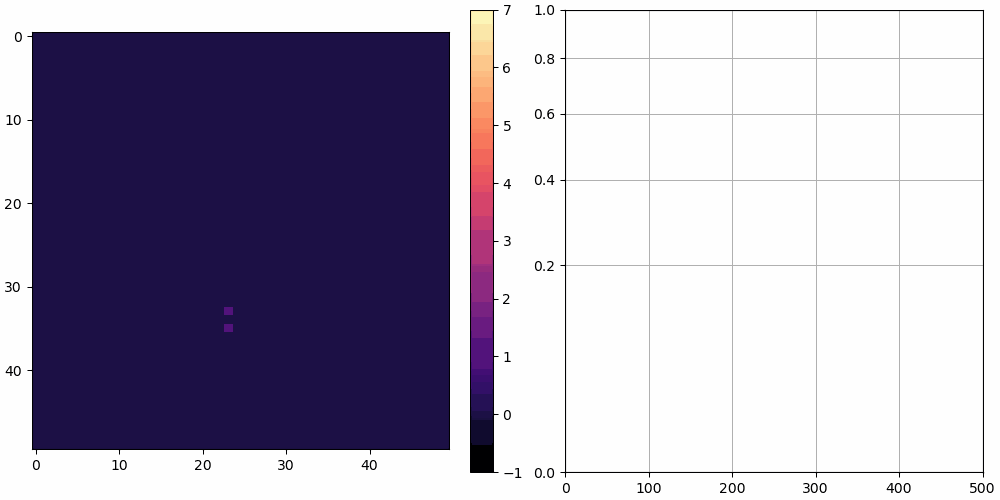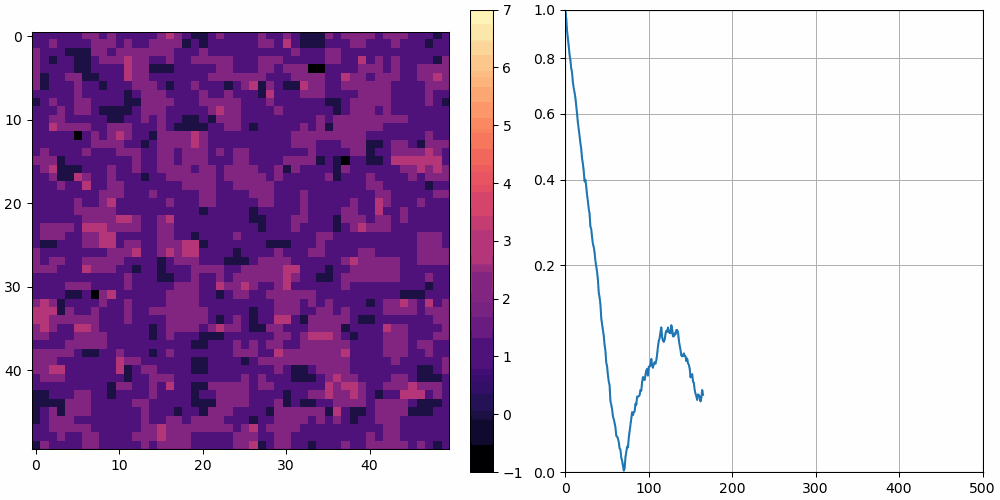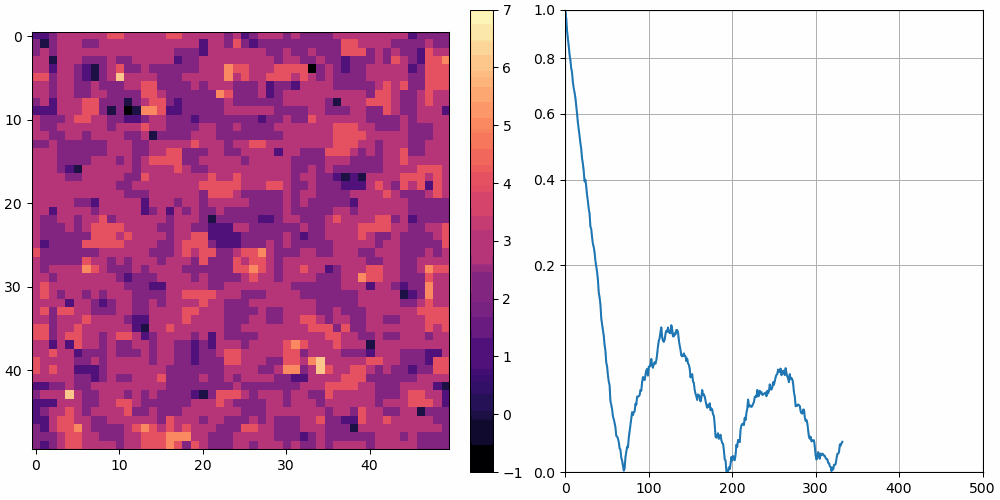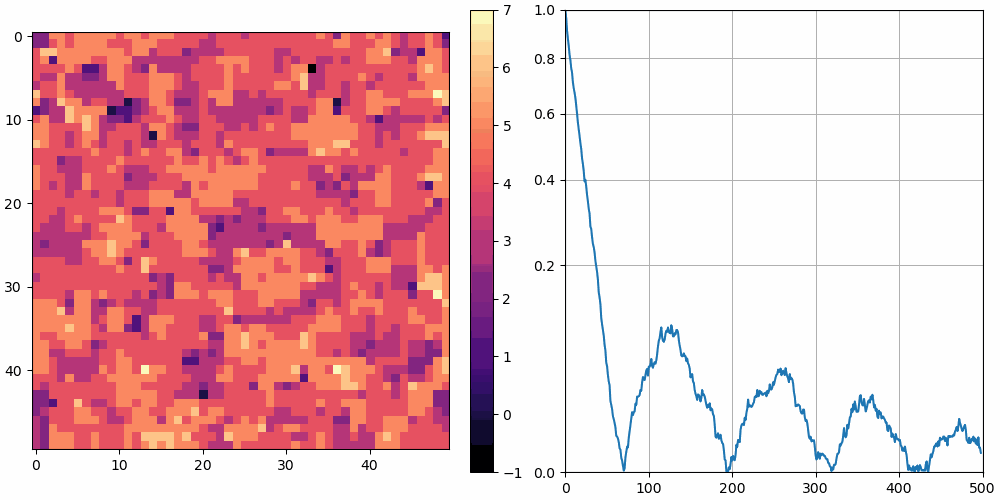
The left shows a heatmap of the surface height, and the right shows $I$ over time. $I$ is plotted using a square root vertical scale, which gives more space for the smaller numbers. Unless otherwise noted, the simulations are animated at 10 frames per second and 10 simulation cycles per frame.

The parameters $j$ and $\frac{E_b}{k_bT}$ can be tuned to change exactly how the growth proceeds. A larger $j$ will result in faster condensation, and a smaller $\frac{E_b}{k_bT}$ will result in faster migration. Note that in real life, $\frac{E_b}{k_bT}$ would be controlled by changing $T$ .

First, let’s see what happens when we change $\frac{E_b}{k_bT}$ when $j=0$ , i.e. there are no atoms arriving from the fluid. The following three simulations have $\frac{E_b}{k_bT}=2$ , $\frac{E_b}{k_bT}=1.5$ , and $\frac{E_b}{k_bT}=1$ :

As $\frac{E_b}{k_bT}$ decreases, you can see more and more atoms leaving their original positions and moving around the surface. In the $\frac{E_b}{k_bT}=1.5$ simulation, you can see the clusters I was talking about earlier. In the $\frac{E_b}{k_bT}=1$ simulation, there are so many atoms moving around that they are piling on top of each other. You can also see that $I$ drops when the simulation starts, settling at lower values for lower values of $\frac{E_b}{k_bT}$ .

Let’s see what happens when we vary $\frac{E_b}{k_bT}$ when $j$ is nonzero. The following simulations have $\frac{E_b}{k_bT}=5$ , $\frac{E_b}{k_bT}=2$ , and $\frac{E_b}{k_bT}=1$ , respectively, and $j=2$ :

Notice that in the $\frac{E_b}{k_bT}=2$ simulation, $I$ is oscillating, but this is not the case in the other two. We can basically identify three regimes in these simulations: when $\frac{E_b}{k_bT}$ is low, the surface grows rough; when it is high, the surface grows rough; and when it is in the middle, the surface grows layer-by-layer.

Next, let’s see what happens when we vary $j$ while $\frac{E_b}{k_bT}$ is fixed. The following two simulations have $j=1$ and $j=5$ , respectively, and $\frac{E_b}{k_bT}=2$ :

Notice how $I$ oscillates. Each oscillation corresponds approximately to 1 atomic layer being added to the surface. The oscillations in the $j=1$ simulation are slower than in the $j=5$ simulation because the atoms are arriving faster in the $j=5$ simulation, so atomic layers are being added faster. The oscillations in the $j=1$ simulation are also more intense than in the $j=5$ simulation. More intense oscillations indicate a smoother surface.

It would be good to speed up the $j=1$ simulation to normalize the rate of oscillations in $I$ to be the same for both simulations. The following 2 animations are also for $j=1$ and $j=5$ , but this time, the $j=1$ simulation has 50 cycles per frame and runs for 5 times more cycles than the $j=5$ simulation:

It appears that increasing $j$ will decrease the smoothness of the surface.

The smoothness of the surface is in part a function of the relative rates of condensation and migration. If migration is faster than condensation, the surface will grow smoothly, since the atoms have plenty of time to form clusters and maintain a flat surface. If condensation is faster than migration, the surface will grow roughly because there is not enough time to form clusters. This is why increasing $j$ decreased the smoothness of the surface, and decreasing $\frac{E_b}{k_bT}$ from 5 to 2 increased the smoothness of the surface.

However, we also saw that decreasing $\frac{E_b}{k_bT}$ from 2 to 1 made the surface rough again. This has to do with something called a roughening transition. If $\frac{E_b}{k_bT}$ is too low (the temperature is too high), entropy takes over and atoms are no longer constrained to form low-energy structures like clusters, and instead pile on top of eachother and form a rough surface.

How do the animations compare to experiment?

If I wanted to look at the motion of atoms on the surface of a crystal, doing a simulation is only one option. I could have tried to directly image the surface of a crystal as it was growing, with a technique like scanning tunneling microscopy (STM). Unfortunately, I don’t have access to a scanning tunneling microscope. Fortunately, other people do, and have used their microscope for this purpose and published the results (Tsukamoto, 2008, see references). Shown below is a series of STM images taken of an indium arsenide crystal as it is being grown:

Like the animations I made, the brighter portions of the image represent areas raised higher up. Every successive image has had another 20% of an atomic layer worth of atoms added to it. The images are 50 nanometers wide, which is about 330 atoms. There is a strong resemblance to some of the animations i’ve shown here, in particular the $\frac{E_b}{k_bT}=2$ and $j=1$ or $2$ animations, with the atoms gathering into clusters which grow and merge into a full layer. One big difference is that there are no isolated atoms visible between the clusters in the STM image. It seems isolated surface atoms are less common in real life than in my simulations (or, maybe they’re not very visible in the STM).

Zooming out

What should one make of this? I have made a number of assumptions for convenience, such as:

Atoms cannot move up or down a step of more than 2
Atoms must break 2 bonds going up or down a step
Atoms do not evaporate from the surface
The rate at which atoms from the fluid stick to the surface is independent of the temperature of the crystal
Atoms only interact with their nearest neighbors
There is no multiplicative factor in front of the exponential in the expression for migration probability

Some of these assumptions are definitely wrong, and the rest are probably wrong as well. It would take more simulations to figure out the degree to which they influence the growth process. One would need to carefully compare experimental data with simulation results to determine which assumptions are accurate.

There are also assumptions I’ve made about the crystal itself:

The crystal consists of a single element
The crystal has a simple cubic structure
The crystal surface is perpendicular to the crystal axis (there is no miscut)
The material growing is the same as the material of the rest of the crystal (homoepitaxy)
the atomic structure on the surface of the crystal is identical to that in the interior of the crystal (there is no reconstruction)

All of these assumptions are frequently and deliberately violated in real life, but incorporating and programming the more realistic conditions would require more effort.

Some of these assumptions would be easy to relax. For example, evaporation could be incorporated by choosing a number of random grid points on the surface and generating an evaporation probability with a similar Arrhenius experssion to the migration probability. A multiplicative factor could be included in front of the exponential in the expression for migration probability, for example, $p=p_0e^{\frac{-nE_b}{k_bT}}$ , which would influence the probability of migration in a different way from $\frac{nE_b}{k_bT}$ , since it’s independent of the number of bonds and appears in front of the exponential instead of in the exponent³.

Footnotes

Yes, a food ingredient. It’s also used for nonlinear optics. ↩︎
I am embarrassed to admit I got the data from C into Python by saving and loading a text file, instead of something more sensible like the C Python API or even just using a binary file. ↩︎
I actually did this at first, but then decided this blog post would be too long if I included it, so I left the multiplicative factor as 1. ↩︎

References

The following are studies that implemented solid-on-solid models in a more rigorous way than me:

F. F. Abraham and G. M. White, Journal of Applied Physics 41, 1841 (1970).

G. H. Gilmer and P. Bennema, Journal of Applied Physics 43, 1347 (1972).

S. Clarke and D. D. Vvedensky, Physical Review Letters 58, 2235 (1987).

P. A. Maksym, Semiconductor Science and Technology 3, 594 (1988).

D. P. Landau and S. Pal, Thin Solid Films 272, 184 (1996).

This is a textbook about molecular beam epitaxy, which contains a lot of good basic information about the theory behind crystal growth, particularly in chapter 6:

J. Y. Tsao, Materials Fundamentals of Molecular Beam Epitaxy (Academic Press, San Diego, 1993).

This is the scanning tunneling microscopy study:

S. Tsukamoto, Hyomen Kagaku 29, 758 (2008)

This is a book chapter about the roughening transition, including a Monte Carlo study not unlike what I did here:

J. D. Weeks, “The Roughening Transition”, in Ordering in Strongly Fluctuating Condensed Matter Systems, edited by T. Riste (Springer US, Boston, MA, 1980), pp. 293–317.